Find Particular and Homogeneous Solution to Boundary Value Problem Fourier

Partial Differential Equations 0.15 alpha

Subsections

5.6.1 The physical problem
5.6.2 The mathematical problem
5.6.3 Outline of the procedure
5.6.4 Step 0: Fix the boundary conditions
5.6.5 Step 1: Find the eigenfunctions
5.6.6 Step 2: Solve the problem
5.6.7 Summary of the solution

5.6 Inhomogeneous boundary conditions

The method of separation of variables needs homogeneous boundary conditions. More precisely, the eigenfunctions must have homogeneous boundary conditions. (Even if in a set of functions each function satisfies the given inhomogeneous boundary conditions, a combination of them will in general not do so.)

In the previous example, this problem could be circumvented by choosing $\theta$ instead of as the variable of the eigenfunctions. For the example in this section, however, this does not work.

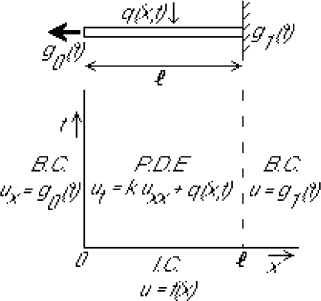
5.6.1 The physical problem

The problem is to find the unsteady temperature distribution in a bar for any arbitrary position and time . The initial temperature distribution at time zero equals a given function . The heat flux out of the left end equals a given function , and the temperature of the right end a given function . Heat is added to the bar from an external source at a rate described by a given function .

**Figure 5.3:** Heat conduction in a bar.
$\begin{figure} \begin{center} \leavevmode {} \epsffile{svb.eps} \end{center} \end{figure}$

5.6.2 The mathematical problem

**Figure 5.4:** Heat conduction in a bar.
$\begin{figure} \begin{center} \leavevmode {} \epsffile{svb1.eps} \end{center} \end{figure}$

5.6.3 Outline of the procedure

We would like to use separation of variables to write the solution in a form that looks roughly like:

$\begin{displaymath} u(x,t) = \sum_n u_n(t) X_n(x) \end{displaymath}$

Here the

would be the eigenfunctions.

The cannot be eigenfunctions since the time axis is semi-infinite. Also, Sturm-Liouville problems require boundary conditions at both ends, not initial conditions.

Unfortunately, eigenfunctions must have homogeneous boundary conditions. So if was simply written as a sum of eigenfunctions, it could not satisfy inhomogeneous boundary conditions.

Fortunately, we can apply a trick to get around this problem. The trick is to write as the sum of a function that satisfies the inhomogeneous boundary conditions plus a remainder :

$\begin{displaymath} u(x,t) = u_0(x,t) + v(x,t) \end{displaymath}$

Since

produces the inhomogeneous term in the boundary conditions, the remainder

satisfies homogeneous boundary conditions. Therefore

can be written as

$\begin{displaymath} v(x,t) = \sum_n v_n(t) X_n(x) \end{displaymath}$

using separation of variables. Add

to get

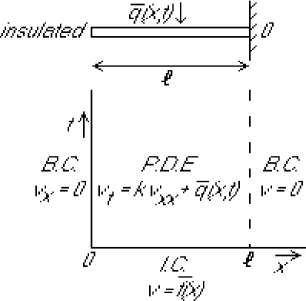
5.6.4 Step 0: Fix the boundary conditions

The first thing to do is find a function that satisfies the same boundary conditions as . In particular, must satisfy:

$\begin{displaymath} u_{0,x}(0,t)=g_0(t) \qquad u_{0}(\ell,t)=g_1(t) \end{displaymath}$

The function does not have to satisfy the either the partial differential equation or the initial condition. That allows you to take something simple for it. The choice is not unique, but you want to select something simple.

A function that is linear in ,

$\begin{displaymath} u_0(x,t) = A(t) + B(t) x \end{displaymath}$

is surely the simplest possible choice. In this example, it works fine too.

Plug this expression for into the boundary conditions for ,

$\begin{displaymath} u_x(0,t)= g_0(t) \qquad u(\ell,t)=g_1(t) \end{displaymath}$

That produces the requirements

$\begin{displaymath} B(t) = g_0(t) \qquad A(t)+ B(t)\ell = g_1(t) \end{displaymath}$

The solution is

and $A(t)=g_1(t)-B(t)\ell$ . So our

$\begin{displaymath} u_0(x,t) = g_1(t)+g_0(t)(x-\ell) \end{displaymath}$

Keep track of what we know, and what we do not know. Since we (supposedly) have been given functions and , function is from now on considered a known quantity, as given above.

You could use something more complicated than a linear function if you like to make things difficult for yourself. Go ahead and use $A(t) {\rm erf}(x)+B(t)J_0(x)$ if you really love to integrate error functions and Bessel functions. It will work. I prefer a linear function myself, though. (For some problems, you may need a quadratic instead of a linear function.)

Under certain conditions, there may be a better choice than a low order polynomial in . If the problem has steady boundary conditions and a simple steady solution, go ahead and take to be that steady solution. It will work great. However, in the example here the boundary conditions are not steady; we are assuming that and are arbitrary given functions of time.

Next, having found , define a new unknown as the remainder when is subtracted from :

$\begin{displaymath} v \equiv u - u_0 \end{displaymath}$

We now solve the problem by finding

. When we have found

, we simply add

, already known, back in to get

To do so, first, of course, we need the problem for to solve. We get it from the problem for by everywhere replacing by . Let's take the picture of the problem for in front of us and start converting.

**Figure 5.5:** Heat conduction in a bar.
$\begin{figure} \begin{center} \leavevmode {} \epsffile{svb1.eps} \epsffile{svb2.eps} \end{center} \end{figure}$

First take the boundary conditions at and $x=\ell$ :

$\begin{displaymath} u_x(0,t)=g_0(t) \qquad u(\ell,t)=g_1(t) \end{displaymath}$

Replacing

$\begin{displaymath} u_{0x}(0,t)+v_x(0,t)=g_0(t) \qquad u_{0}(\ell,t)+v(\ell,t)=g_1(t) \end{displaymath}$

But since by construction $u_{0x}(0,t)=g_0$ and $u_{0}(\ell,t)=g_1$ ,

$\begin{displaymath} v_x(0,t)=0 \qquad v(\ell,t)=0 \end{displaymath}$

Note the big thing: while the boundary conditions for

are similar to those for

, they are homogeneous. We will get a Sturm-Liouville problem in the

-direction for

where we did not for

. That is what

does for us.

We continue finding the rest of the problem for . We replace by into the partial differential equation $u_t=\kappa u_{xx}+q$ ,

$\begin{displaymath} u_{0,t} + v_t = \kappa (u_{0,xx} + v_{xx}) + q \end{displaymath}$

and take all

terms to the right hand side:

$\begin{displaymath} v_t = \kappa v_{xx} + \bar q \end{displaymath}$

where $\bar q = \kappa u_{0,xx} + q -u_{0,t}$ , or, written out

$\begin{displaymath} \fbox{$\displaystyle \bar q(x,t) = q(x,t) - g_1'(t) - g_0'(t)(x-\ell) $} \end{displaymath}$

Hence $\bar q$ is now a known function, just like

The final part of the problem for that we have not converted yet is the initial condition. We replace by in ,

$\begin{displaymath} u_0(x,0) + v(x,0) = f(x) \end{displaymath}$

and take

to the other side:

$\begin{displaymath} v(x,0) = \bar f(x) \end{displaymath}$

where $\bar f(x)$ is

, or written out:

$\begin{displaymath} \fbox{$\displaystyle \bar f(x) = f(x) - g_1(0) - g_0(0)(x-\ell) $} \end{displaymath}$

Again, $\bar f$ is now a known function.

The problem for is now the same as the one for , except that the boundary conditions are homogeneous and functions and have changed into known functions $\bar f$ and $\bar q$ .

Using separation of variables, we can find the solution for in the form:

$\begin{displaymath} v(x,t) = \sum_n v_n(t) X_n(x). \end{displaymath}$

We already know how to do that! (Don't worry, we will go over the steps anyway.) Having found

, we will simply add

to find the asked temperature

5.6.5 Step 1: Find the eigenfunctions

To find the eigenfunctions , substitute a trial solution into the homogeneous part of the partial differential equation, $v_t = \kappa v_{xx} + \bar q$ . Remember: ignore the inhomogeneous part $\bar q$ when finding the eigenfunctions. Putting into $v_t = \kappa v_{xx}$ produces:

$\begin{displaymath} T'X = \kappa T X'' \end{displaymath}$

Separate variables:

$\begin{displaymath} \frac{T'}{\kappa T} = \frac{X''}{X} = \hbox{ constant } = - \lambda \end{displaymath}$

As always, $\lambda$ cannot depend on

since the left hand side does not. Also, $\lambda$ cannot depend on

since the middle does not. So $\lambda$ must be a constant.

We then get the following Sturm-Liouville problem for any eigenfunctions :

$\begin{displaymath} - X'' = \lambda X \qquad X'(0) = 0 \qquad X(\ell)=0 \end{displaymath}$

The last two equations are the boundary conditions on

which we made homogeneous.

This is the exact same eigenvalue problem that we had in an earlier example, so I can just take the solution from there. The eigenfunctions are:

$\begin{displaymath} \fbox{$\displaystyle \lambda_n = \frac{(2n-1)^2 \pi^2}{4... ...(2n-1) \pi x}{2\ell}\right) \qquad (n = 1, 2, 3, \ldots) $} \end{displaymath}$

5.6.6 Step 2: Solve the problem

We expand in the problem for in a Fourier series:

**Figure 5.6:** Heat conduction in a bar.
$\begin{figure} \begin{center} \leavevmode {} \epsffile{svb2.eps} \end{center} \end{figure}$

In particular,

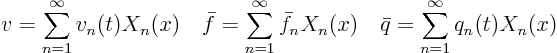
$\begin{displaymath} v = \sum_{n=1}^\infty v_n(t) X_n(x) \quad \bar f = \sum_... ...r f_n X_n(x) \quad \bar q = \sum_{n=1}^\infty q_n(t) X_n(x) \end{displaymath}$

Since $\bar q(x)$ and $\bar f(x)$ are known functions, we can find their Fourier coefficients from orthogonality:

$\begin{displaymath} \bar f_n = \frac {\int_0^\ell \bar f(x) X_n(x){ \rm d}x} {\int_0^\ell X_n^2(x){ \rm d}x} \end{displaymath}$

$\begin{displaymath} \bar q_n(t) = \frac {\int_0^\ell \bar q(x,t) X_n(x){ \rm d}x} {\int_0^\ell X_n^2(x){ \rm d}x} \end{displaymath}$

or with the eigenfunctions written out

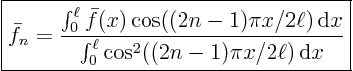
$\begin{displaymath} \fbox{$\displaystyle \bar f_n = \frac {\int_0^\ell \ba... ...m d}x} {\int_0^\ell \cos^2((2n-1)\pi x/2\ell){ \rm d}x} $} \end{displaymath}$

$\begin{displaymath} \fbox{$\displaystyle \bar q_n(t) = \frac {\int_0^\ell ... ...m d}x} {\int_0^\ell \cos^2((2n-1)\pi x/2\ell){ \rm d}x} $} \end{displaymath}$

The integrals in the bottom equal $\frac12\ell$ .

So the Fourier coefficients $\bar f_n$ are now known constants, and the $\bar q_n(t)$ are now known functions of . Though in actual application, numerical integration may be needed to find them. During finals, I usually make the functions , and simple enough that you can do the integrals analytically.

Now write the partial differential equation $v_t = \kappa v_{xx} + \bar q$ using the Fourier series:

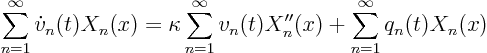
$\begin{displaymath} \sum_{n=1}^\infty \dot v_n(t) X_n(x) = \kappa \sum_{n=1}^\infty v_n(t) X_n''(x) + \sum_{n=1}^\infty q_n(t) X_n(x) \end{displaymath}$

Looking in the previous section, the Sturm-Liouville equation was $-X''=\lambda X$ , so the partial differential equation simplifies to:

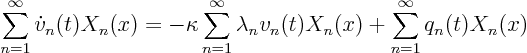
$\begin{displaymath} \sum_{n=1}^\infty \dot v_n(t) X_n(x) = - \kappa \sum_{n=... ...y \lambda_n v_n(t) X_n(x) + \sum_{n=1}^\infty q_n(t) X_n(x) \end{displaymath}$

It will always simplify or you made a mistake.

For the sums to be equal for any , the coefficients of every individual eigenfunction must balance. So we get

$\begin{displaymath} \dot v_n(t) + \kappa \lambda_n v_n(t) = q_n(t) \end{displaymath}$

We have obtained an ordinary differential equation for each

. It is again constant coefficient, but inhomogeneous.

Solve the homogeneous equation first. The characteristic polynomial is

$\begin{displaymath} k + \kappa \lambda_n = 0 \end{displaymath}$

so the homogeneous solution is

$\begin{displaymath} v_{nh} = A_n e^{-\kappa\lambda_n t} \end{displaymath}$

For the inhomogeneous equation, undetermined constants is not a possibility since we do not know the actual form of the functions . So we use variation of parameter:

$\begin{displaymath} v_n = A_n(t) e^{-\kappa\lambda_n t} \end{displaymath}$

Plugging into the ordinary differential equation produces

$\begin{displaymath} A_n' e^{-\kappa\lambda_n t} + 0 = q_n(t)\quad \Longrightarrow\quad A_n' = q_n(t) e^{\kappa\lambda_n t} \end{displaymath}$

We integrate this equation to find

. I could write the solution using an indefinite integral:

$\begin{displaymath} A_n(t) = \int q_n(t) e^{\kappa\lambda_n t} { \rm d}t \end{displaymath}$

But that has the problem that the integration constant is not explicitly shown. That makes it impossible to apply the initial condition. It is better to write the anti-derivative using an integral with limits plus an explicit integration constant as:

$\begin{displaymath} A_n(t) = \int_{\tau=0}^t q_n(\tau) e^{\kappa\lambda_n \tau} { \rm d}\tau + A_{n0} \end{displaymath}$

You can check using the Leibniz rule for differentiation of integrals (or really, just the fundamental theorem of calculus,) that the derivative is exactly what it should be. (Also, the lower limit does not really have to be zero; you could start the integration from 1, if it would be simpler. The important thing is that the upper limit is the independent variable

Putting the found solution for into

$\begin{displaymath} v_n = A_n(t) e^{-\kappa\lambda_n t} \end{displaymath}$

we get, cleaned up:

$\begin{displaymath} v_n(t) = \int_{\tau=0}^t q_n(\tau) e^{-\kappa \lambda_n(t - \tau)} { \rm d}\tau + A_{n0} e^{-\kappa\lambda_n t} \end{displaymath}$

We still need to find the integration constant $A_{n0}$ . To do so, write the initial condition $v(x,0) = \bar f(x)$ using Fourier series:

$\begin{displaymath} \sum_{n=0}^\infty v_n(0) X_n(x) = \sum_{n=0}^\infty \bar f_n X_n(x) \end{displaymath}$

This gives us initial conditions for the

$\begin{displaymath} v_n(0) = \bar f_n = A_{n0} \end{displaymath}$

the latter from above, and hence

$\begin{displaymath} v_n(t) = \int_{\tau=0}^t q_n(\tau) e^{-\kappa \lambda_n(t - \tau)} { \rm d}\tau + \bar f_n e^{-\kappa\lambda_n t} \end{displaymath}$

or writing out the eigenvalue:

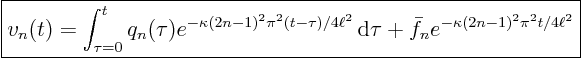
$\begin{displaymath} \fbox{$\displaystyle v_n(t) = \int_{\tau=0}^t q_n(\tau) ... ...,\rm d}\tau + \bar f_n e^{-\kappa (2n-1)^2\pi^2 t/4\ell^2} $} \end{displaymath}$

We have

in terms of known quantities, so we are done.

5.6.7 Summary of the solution

Collecting all the boxed formulae together, the solution is found by first computing the coefficients $\bar f_n$ from:

$\begin{displaymath} \bar f_n = \frac2\ell {\int_0^\ell \bar f(x)\cos((2n-1) \pi x/2\ell){ \rm d}x} \qquad (n=1,2,3,\ldots) \end{displaymath}$

where

$\begin{displaymath} \bar f(x) = f(x) - g_1(0) - g_0(0)(x-\ell) \end{displaymath}$

Also compute the functions $\bar q_n(t)$ from:

$\begin{displaymath} \bar q_n(t) = \frac2\ell {\int_0^\ell \bar q(x,t)\cos((2n-1)\pi x/2\ell){ \rm d}x} \qquad (n=1,2,3,\ldots) \end{displaymath}$

where

$\begin{displaymath} \bar q(x,t) = q(x,t) -g_1'(t) - g_0'(t)(x-\ell) \end{displaymath}$

Then the temperature is:

$\begin{displaymath} \begin{array}{l} \displaystyle u(x,t)_{\strut} = g_1(t... ...ll^2} \right] \cos\frac{(2n-1)\pi x}{2\ell} \end{array} \end{displaymath}$

Find Particular and Homogeneous Solution to Boundary Value Problem Fourier

Source: https://eng-web1.eng.famu.fsu.edu/~dommelen/pdes/style_a/svbex.html

Schlapp Antaistry